A single worth utilized to symbolise an entire set of information is called the Procedure of Central Propensity In contrast to other worths, it is a common worth to which most of observations are more detailed. The expected value is one method to determine main propensity in data. This procedure of main propensity includes the condensation of a big quantity of information to a single worth.
For example, the typical weight of the 10 trainees in the class is 50 kg. Nevertheless, one trainee weighs 28 kg, another trainee weighs 56 kg, and so on. This suggests that 50 kg is the one worth that represents the typical weight of the class and the worth is more detailed to most of observations, which is called mean.
In reality, the value of showing a single worth for a big quantity of information makes it easy to take a look at and evaluate a set of information and deduce needed info from it. The expected value is computed by dividing the overall worth of all observations by the overall variety of observations. It is typically described as Mean or Typical by individuals in basic and is typically represented by the letter XÌ.
Estimation of Expected Value in Diplomatic Immunities
The computation of the Mean differs under specific diplomatic immunities such as:
1. Cumulative Series (Less than or More than):
Cumulative frequency circulation describes information that is revealed as Less Than or More Than for all products in the series. Such cumulative frequency circulation requires to be become an easy frequency circulation so regarding identify the expected value.
Example:
Determine the typical marks utilizing the list below circulation of 60 trainees’ mathematics marks.
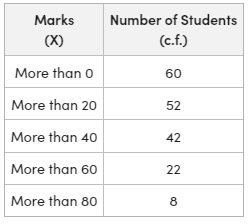
Service:
To compute the mean, first off, alter the provided circulation into easy frequency circulation and discover the frequencies from the provided cumulative frequencies. Then identify the mean of the series utilizing any of the techniques of determining the mean in constant series.
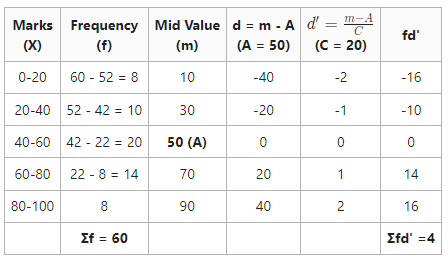
![]()
![]()
Mean = 51.3
2. Mid-Value Series:
The very same technique will be utilized to get the expected value as when it comes to discrete series when mid-values are offered in the concern of a constant series (instead of class periods).
Example:
Learn the mean of the following information:
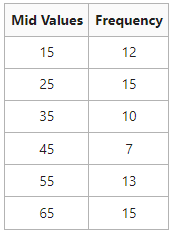
Service:
In the provided example, the mid worths are provided. So the mean can be computed utilizing these mid worths and there is no requirement to transform it into class periods.
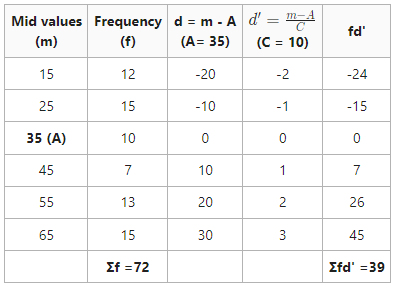
![]()
![]()
Mean = 40.41
3. Inclusive Series:
When providing information as an inclusive series, there is no requirement to alter the classes considering that the mid-value will remain constant despite any modifications made. There is no requirement to transform inclusive class periods into special classes.
Nevertheless, it is needed to transform the inclusive series into the special series if one requires to identify the typical and mode.
Example:
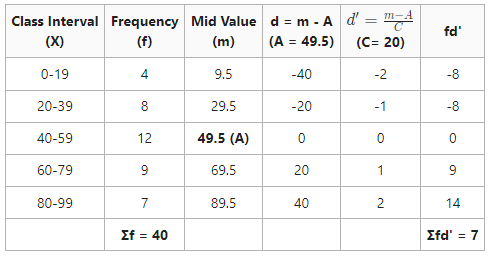
Learn the mean of the following information:
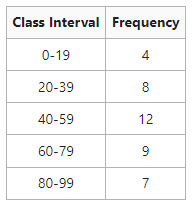
Service:
In this provided case, inclusive class periods are not transformed into special class periods to compute the mean.
![]()
![]()
Mean = 53
4. Open-end Series:
Open-end class periods are those without a lower limitation for the very first class period and a ceiling for the last class period.
In this case, the mean can not be identified without presuming the missing out on class limitations. The pattern of class periods in other classes impacts the missing out on worths. There might be some problem in identifying the limitations of the open-ended classes if the defined class periods are not equivalent. In such cases, limitations need to be presumed on some logical basis.
Example:
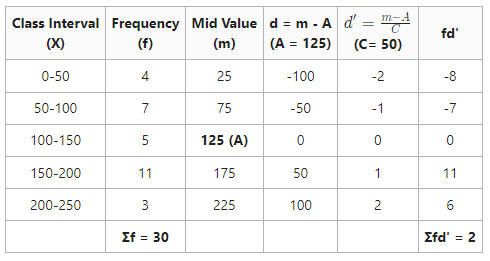
Determine the mean of the following information.
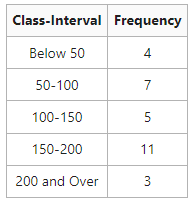
Service:
In the above example, class periods are consistent; i.e., there is a space of 50 in each class period. So, it can be presumed that open-end class periods are likewise comparable to 50. Therefore, the lower limitation of the very first class period is 0 (0-50) and the ceiling of the last class period is 250 (200-250). The mean can now be computed.
![]()
![]()
Mean = 128.33
5. Unequal Class-Intervals:
Often the class periods in the circulation might not be uniformly dispersed. After calculating the mid-points of each period, the mean can be computed utilizing any of the techniques of determining the mean. It indicates that class periods are not made equivalent.
Example:
Determine the mean of the following information.
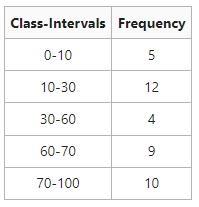
Service:
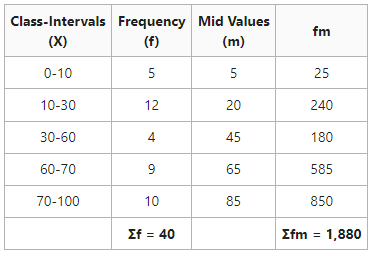
The mean can be computed straight without making any modification in the above class periods.
![]()
![]()
Mean = 47
Last Upgraded:
31 Jul, 2023
Like Post
Conserve Post